Volume : 1 | Issue : 1
Conceptual Paper
Sample size calculation in cluster randomization clinical trials
Manoj Kumar Yadav
IQVIA, India
Received: February 02, 2018 | Published:February 21, 2018
Abstract
The question of sample size is basic to the planning of any clinical study. When a survey is carried out using cluster sampling, between-cluster variation at each level of sampling contributes an additional source of variation, which must be allowed for in addition to between-subjects i.e. within cluster variation, to validly estimate parameters or to test their significance. The number of subjects needed for a cluster randomization trail is larger than for a study of the same power in which individual subjects are randomly sampled. In this paper, the illustrations are done to quantify the impact of increasing intraclass correlation on sample size.
Keywords: Cluster randomized trials; Intraclass correlation coefficient; Variation inflation factor; Sample size calculation; Clinical research
Introduction
Cluster randomization trials (CRTs) are experiments in which entire social units or clusters of subjects rather than independent subjects are randomly allocated to intervention groups. For e.g. villages are selected as the randomization unit in clinical trials evaluating the efficacy of disease screening programs and schools are selected as the randomization unit in trials evaluating impact of nutritional pills on children’s health. Randomizing individuals to treatments is not always feasible and cluster randomized trials are increasingly being utilized in the evaluation of health care interventions.1 In school-based smoking intervention studies, randomization of schools rather than students to different treatment conditions is the usual approach to sampling.2,3 CRTs are gaining popularity in health research to deal with large scale population surveys. There are few challenges in designing the CRTs, one, who may provide consent on behalf of a particular group and on what authority they may do so, another, in CRTs, the units of randomization and observation may not be the same, the group that receives the experimental treatment may not be the same as the group from which data are collected. For e.g. in trial assessing the surgical efficiency of two surgical instruments, surgeons are randomized to use surgical instruments by collecting post-operative pain scores on patients operated by surgeons. Weijer et al. have discussed these challenges in designing CRTs, the research community and regulators are persistently working on to conquer these challenges.4 This research work is dedicated to address one of the challenge in calculating sample size for CRTs.
Intraclass correlation coefficient
The intraclass correlation coefficient (ICC) measures the degree of similarity among responses within the same cluster. This parameter may be interpreted as the standard Pearson's correlation coefficient between any two responses in the same cluster. In designing cluster-based randomized trials or intervention studies, accurate estimates of ICCs are required for sample size calculation to achieve desired power. In my earlier research, the ICCs at two and three levels have been illustrated in detail.5,6
Variation inflation factor
Variation inflation factor (VIF) is the ratio of the variance of an overall sample mean estimated from cluster means to the variance of an overall sample mean estimated from subjects within clusters. Generally VIF is a function of the average cluster size and the intraclass correlation coefficient (ICC) for the outcome variable under study i.e. where is the average number of subjects per cluster and is the ICC for the outcome variable. To estimate the required sample size, the design effect or variation inflation factor (VIF) must be incorporated into the sample-size calculation.7 In my earlier research, the VIF at two and three levels have been illustrated in detail.5,6
Concepts
Consideration of units to be independent leads the situation of ignoring the variability at higher levels, thus having inferences with inflated power.1,8-11 Nesting implies violation of the assumptions of independence of observations and ignoring this dependency in data yields inflated test statistics when observations are correlated.
Decisions have to be made first about the number of clusters which should be selected and second the number of units which should be selected from each cluster. Even very small ICC values may have a big impact on sample-size estimation. Several authors have discussed how to use ICC estimates in calculating the number of clusters needed per treatment to detect a treatment effect. It is illustrated below the use of the ICC estimates for sample-size calculation in testing the hypothesis about the difference between means of two treatment groups. Type I error is fixed at , and we want the test to have power . If we were using simple random sampling (SRS), the sample size required would be:
Here, is the number of subjects required per treatment group, and are the values of standard normal variate for which the probability of smaller values is and respectively, is the variance (assumed common) in each treatment group, and is the difference in either direction in the treatment means which we would want to detect. If we fix the number of subjects per cluster at ‘ ’, the number of clusters ‘ ’ required using SRS will be obtained from the above formula, by taking . To take into account the intraclass correlation, we have to multiply the variance by a factor of , the variation inflation factor. The number of clusters required using cluster sampling for each treatment group will be:
Illustrations
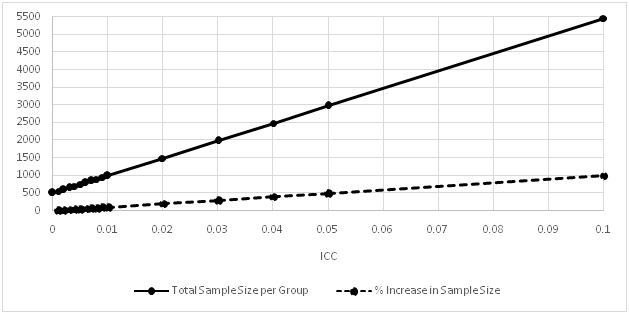
This is the simulated case study to calculate sample size in a cluster randomization clinical trial to assess the effect of nutrients on height in infants completing 3 years. To detect the difference of 1.1 inches (34.5 and 33.4 inches in treatment and placebo groups respectively) with 6.2 inches of common standard deviation in both treatment groups with 5% type I error, Table 1 presents the total sample size per group with increasing ICC to achieve 80% power by considering 100 infants in each cluster, hence 100 is the average number of subjects per cluster.
| Case | ICC | VIF | Total Sample Size per Group | % Increase in Sample Size as Compared to SRS |
|---|---|---|---|---|
| 1 | 0.000 | 1.000 | 500 | SRS Case |
| 2 | 0.001 | 1.099 | 550 | 10 |
| 3 | 0.002 | 1.198 | 599 | 20 |
| 4 | 0.003 | 1.297 | 649 | 30 |
| 5 | 0.004 | 1.396 | 698 | 40 |
| 6 | 0.005 | 1.495 | 748 | 50 |
| 7 | 0.006 | 1.594 | 797 | 59 |
| 8 | 0.007 | 1.693 | 847 | 69 |
| 9 | 0.008 | 1.792 | 896 | 79 |
| 10 | 0.009 | 1.891 | 946 | 89 |
| 11 | 0.010 | 1.990 | 996 | 99 |
| 12 | 0.020 | 2.980 | 1491 | 198 |
| 13 | 0.030 | 3.970 | 1986 | 297 |
| 14 | 0.040 | 4.960 | 2481 | 396 |
| 15 | 0.05 | 5.950 | 2977 | 495 |
| 16 | 0.100 | 10.900 | 5453 | 991 |
Table 1 Sample size calculation with increasing ICC.
Discussion and conclusions
By focusing on Table 1, case 1 with ICC=0 represents the SRS and total sample size per group is 500. Based on this SRS case, the sample size and % increase in sample size with respect to SRS is calculated with increasing ICC. In case 2, even a very small ICC=0.001, increases the sample size by 10%, almost same amount of increment in sample size is evident with an increase in sample size by 0.001. In case 11, ICC=0.01 increases total sample size by almost two fold. In case 16, ICC=0.1 increases the sample size by almost 10 fold. Figure 1 showing an increasing trend, depicts the impact of increasing ICC on sample size. Conclusively, role of even a very small ICC can’t be ignored while designing the CRTs. To draw inferences from cluster randomized clinical trials, more sample size is required to produce the same power as compared to SRS schemes. The VIF and ICCs have to be supplemented into sample size calculations in order to furnish precise sample size to meet power requirement.
Acknowledgements
This research work is dedicated to my late grandfather Shudarshan Lal Yadav and his two brothers Kanhaiyaa Lal Yadav, Sardar Singh Yadav who created my endless interest in research. Special thanks goes to my PhD supervisor Prof. G. G. Agarwal. The suggestions and comments from two anonymous referees contributed greatly to improve the final manuscript.
References
- Donner A, Klar N. Design and analysis of cluster randomization trials in health research. London Arnold. 2000.
- Murray DM, Hannan PJ. Planning for the appropriate analysis in school-based drug-use prevention studies. J Consult Clin Psychol. 1990;58(4):458−468.
- Donner A. A regression approach to the analysis of data arising from cluster randomization. Int J Epidemiol. 1985;14(2):322−326.
- Weijer C. Ethical issues posed by cluster randomized trials in health research. Trials. 2011;12:100.
- Yadav MK, Agarwal GG. On Estimation of standard error of intra-class correlation coefficient in unbalanced nested designs. Commun Stat Theory Methods. 2013;42:88−97.
- Yadav MK. Estimating standard error of intra-class correlation coefficients up to three level unbalanced nested clinical trials. Commun Stat Theory Methods. 2016;44(22):6688−6699.
- Kish L. Survey sampling. New York: John Wiley & Sons, Inc. 1965.
- Snijders AB, Bosker RJ. Multilevel analysis: an introduction to basic and advance level multilevel modeling. London: Sage. 1999.
- Agarwal GG, Awasthi S, Walter SD. Intra-class correlation estimates for assessment of vitamin A intake in children. J Health Popul Nutr. 2005;23(1):66−73.
- Siddiqui O, Hedeker D, Flay BR, et al. Intraclass correlation estimates in school-based smoking prevention study. Am J Epidemiol. 1996;144(4):425−433.
- Gulliford MC, Ukoumunne OC, Chinn S. Components of variance and intraclass correlations for the design of community-based survey and intervention studies. Am J Epidemiol. 1999;149(9):876−883.