Abstract

Objective: The objectives of this study are: 1.) To calculate the probability of Cardiovascular Disease (CVD) events by applying three different equations, which are: the Asia-Pacific Cohort Study (APCS) equation, the Framingham-Asia equation and the original Framingham equation, to the individual risk factors data from the NHESIV, Thailand. 2) To estimate the number of 8-10 years CVD events. 3) To validate and identify the most suitable CVD risk equations for the Thai population. The individual risk factors from the NHESIV dataset was entered into a Microsoft Excel spreadsheet as the baseline population.

Methods: Asia-Pacific Collaborative Cohort Study (APCCS) equations, the Framingham-Asia equation and the original Framingham equation, are applied to calculate the probability of 8 to 10 years CVD events by age groups and gender. The CVD events in this analysis refer to all fatal and non-fatal CVD events (ICD10, I00-I99), which include Ischemic heart disease (IHD) (ICD10, I20-I25) and stroke (ICD10, I60-I69).

Results: The 4th National Health Examination Survey IV 2009 (NHESIV) dataset has been entered into a Microsoft Excel spreadsheet as the baseline population. APCCS, the Framingham-Asia and the original Framingham equations, were applied to the NHESIV dataset. The APCCS equation calculated the average 8-years probability of getting CVD as 8.3% in men and 7.8% in women. The 8-year likelihood of CVD in the Framingham-Asia equation was 7.2% in men and 8.1% in women. The original Framingham equation showed the highest probability of 10-years CVD which were 18.8% in men and 11.1% in women.

Conclusions: The original Framingham equation overestimated the risk of CVD in the Thai population in all age groups. The Asia-Pacific Cohort Study (APCCS) and the Framingham-Asia equations, both performed better estimation than the original Framingham equation in both men and women.

Keywords: Cardiovascular Disease (CVD), Asia-Pacific Collaborative Cohort Study, (APCCS) equations, Framingham-Asia equations

Introduction

Cardiovascular disease (CVD), a set of disease affecting either the heart or blood vessels, is a global health problem, the prevalence of which has led to an increased epidemiological transition of the disease from high-income countries to low-middle income countries. CVD risk prediction models have been developed in many studies, as a tool to predict the levels of CVD in the future. The most influential prediction models, using statistical multivariate analysis equations, were derived from the Framingham Study.^1–4 Many studies found that the Framingham's function was suitable for predicting future CVD in the middle-aged, US white population and others with similar profiles of CVD risks.^5,6 However, some studies showed an overestimated prediction for groups which have different risk profiles and ethnicity such as Asian and some EU populations.^7–10

Nevertheless, the Framingham equation gives a generalised prediction, concerning the biomarker risk factors, such as blood pressure and cholesterol level. Several studies have developed adjustments to the Framingham CVD risk prediction equation, to adapt it for use in specific populations. For example, the QRISK(cardiovascular risk calculator) score in the United Kingdom and the Asia Pacific Collaborative Cohort Studies (APCCS).^11,12 In Thailand, to date, there is only one CVD risk score, which has been derived from the EGAT cohort study.¹³ This study has followed-up 3,499 participants aged 35 to 54 years since 1985. Several studies found that RAMA-EGAT risk score provided a better prediction of CVD than the Framingham equation.¹⁴ Although the CVD risk score was derived specifically for the Thai population, this cohort study was well representative only for Thai middle-class men aged 35 years and over, but it was not well represented in women.¹

Given the limitation of the CVD risk equations for the Thai population, the objectives of this study are: 1) To calculate the probability of CVD events using the three difference equations, namely: the APCS equation, the Framingham-Asia equation and the original Framingham equation, to the individual risk factors data from the NHS, Thailand; 2) To estimate the number of 8-10 years CVD events; 3) To identify and validate the most suitable CVD risk equations for the Thai population.

This research presents the results of the application of the CVD risk assessment equations to the Thai populations and the probability of CVD events using the three different equations, the estimated number of non-fatal CVD events in the Thai people and the validation of the mathematic model. The details of the analysis and CVD risk assessment equations have been described in the previous study.

Materials and Methods

The 4^th National Health Examination Survey IV (NHESIV), 2009 dataset has been used as the baseline population and provided the risk factors profile of the Thai population. This survey represents the prevalence of chronic diseases and the potential health risk factors to the Thai population. This survey is a national representative of the Thai health status by age, gender, administrative area (urban/rural) and geographic regions. The NHESIV dataset has been used as the study population.

Calculation of the CVD probability

The individual data and risk factors profile has been entered to an Excel spreadsheet. The APCS, Framingham-Asia and the original-Framingham equations have been applied to the data to calculate the probability of getting CVD in each. Then, the mean of 8-10 years probability has been calculated by age groups and gender. The primary outcomes are the probability of IHD, stroke and all CVD events. The Asia-Pacific Collaborative Cohort Study equations (APCS equation), had used the concept of the Cox's proportional hazard model, which had been derived from 172,077 participants of the cohort studies around Asia and 25,682 Chinese cohorts. The Electricity Generating Authority of Thailand (EGAT) cohort studies also included in this APCS (Asia Pacific Cohort Studies Collaboration et al. 2007).¹⁵ Second, the recalibrated Framingham’s equation or the low information Framingham’s equation (Framingham Asia), has applied the Cox's proportional hazard model concept derived from 6,053 participants of the Framingham studies and adjusted for the Asian population, where some risk data is not available (Asia Pacific Cohort Studies Collaboration et al. 2007).¹⁵ Third, the Framingham’s equation (Framingham original), using the concept of the Weibull accelerated failure-time models, which have been applied to the Thai population.¹⁶ The main outcome prediction is the of probabilities of CVD related events, such as stroke, heart attacks and heart failure. Details of the equations and the process of calculations are described in the appendix.

Outcome of interests

8 to 10 years probability of getting CVD, IHD or Stroke of the individuals and the 8 to 10 years probability of getting CVD, IHD or Stroke events by age groups and gender. 

Estimated number of CVD events

The number of CVD events at the national level is estimated by multiplying the CVD probability to the number of the mid-year population in 2009, by age groups and gender, to obtain the number of all CVD events over the next 8 to 10 year period. The probability of CVD events includes both fatal and non-fatal CVD.  The analysis excluded those who died based on the statistical information. The model deducted the number of people who are likely to die from CVD, which will estimate the number of people who are alive with the CVD conditions. The probability of dying from a CVD condition is calculated from the national CVD mortality rate in Thailand, from the national statistical report over the past decade.

Validation of the CVD estimated events

The estimated number of CVD events are validated with the actual number of CVD hospital admissions in Thailand in 2009. The number of CVD cases are classified by the ICD-10 code in which I0-I99 refers to all CVD events, I20-I25 refers to IHD and I60-I69 relates to stroke. The actual number of CVD admissions comes from the National Health Security Office, Thailand (NSO) which covers 75% of all hospital admissions in Thailand and includes the patients who were in the universal coverage health care scheme.

Results

The probability of CVD events

Table ‎1 shows the comparison of the mean likelihood of CVD, which has been calculated by using the APCS equation, the Framingham-Asia equation and the original Framingham equation in the NHESIV dataset. The mean probability of CVD has been estimated by age groups and gender. 

When applying the APCCS equation, the overall mean of 8-year CVD probability is 8.3% in men and 7.8% in women. The trend of 8-year probability increased according to age groups in both men and women. The likelihood of CVD is lowest at age 15-24 years, and the possibility of CVD starts to grow from the 45-54 years age group The CVD probability in men is higher than in women from the ages 15 to 74 years; whereas, women have CVD probability higher than men at age 75 years and over.

The mean 8-year probabilities of CVD when using the Framingham-Asia equation are 7.2% in men and 8.1% in women. The minimum CVD probability is at age 15-24 year. At age 45-54 years, the CVD probability in men is 3.2% and 2.6% in women. The CVD probability is equal to 6.7% in both men and women at age 55-64 years. The CVD probability increases with an increase of age groups. Although the trends of CVD probability of the Framingham-Asia equation are similar to the CVD probability that is calculated with APCS equation, the Framingham-Asia calculated the CVD probability in women as higher than in men from age 65 years and over. The 8-year probability of CVD is highest at age 75 years and over.

Regarding the original Framingham equation, the overall mean of 10-year CVD probability is 18.8% in men and 11.1% in women. The CVD probability in men is higher than in women in all age groups. The lowest CVD probabilities are 1.9% in men and 0.8% in women at age 15-24 years. The CVD probability continuously increases when age increases, in both men and women. The CVD probability is two times higher in men than in women at the age 35-44 and 45-54 years. In old age groups, the 10-year CVD probability is higher than in the younger age groups, and the highest likelihood of CVD is at age 75 years and over, which are 47.6% in men and 30.8% in women.

Table 2 shows the 10-year probabilities of CVD, which are calculated by the Framingham original equation in the NHESIV data set. This equation is capable of calculating three events, which are IHD, stroke, and all CVD events. Table 2 presents the mean 10-year probability, by CVD condition, age groups and gender.

The overall mean of 10-year IHD probability is 14.5% in men and 8.0% in women. The trend of IHD probability rises with an increase in age groups. Men have more likelihood of getting IHD than women in all age groups. The IHD probability is the lowest at age 15-24, which are 1.9% in men and 0.7% in women. The likelihood of IHD at age 25-34 is 3.9% in men and 1.4% in women. The IHD probability in men continually increases in the middle period and elderly age groups. At age 35-44 years, the IHD probability in men is nearly triple that in women, which is 6.3% in men and 2.4% in women. The IHD probability is twice as high in men as in women at age 45-54 years, which is 10.2% in men and 4.8% in women. At age 55-64, the IHD probability in men is 15.9% and 9.1% in women. The IHD probability in elderly age groups, 65-74 years and 75 years and above is higher than the IHD probability in younger age groups. At age 65-74 years, there are 22.8% of men and 14.0% of women who have a chance of getting IHD. The IHD probability reaches the highest at age 75 years and over, which is 32.4% in men and 20.15 in women.

The average 10-years probability of stroke is 6.2% in men and 3.8% in women. The graph shows that the stroke probability is below 1% from age 15 to 44 years in both men and women. At age 45 – 54 years, there is 1.5% probability in men and 1.2% of women who suffer a stroke. The trend of stroke probability increase from the age of 55 years and men are more likely to have a chance of suffering a stroke than women.  The stroke probability is 4.5% in men and 3.1% in women at age 55-64 years. Then, the stroke probability increases in the elderly age groups, which is 10.6% in men and 6.8% in women at age 65-74 years. The stroke probability reaches 24.7% in men and 14.6% in women at age 75 years and above. Compared to figure 5.3, the mean of the 10-year likelihood of stroke is lower than the probability of IHD, in both men and women in all age groups. The overall mean of stroke probability is twice as high as the mean of IHD probability. In men, the likelihood of IHD is 14.5% and stroke 6.2%. In women, the possibility of IHD is 8.0%, while the chance of stroke is 3.8%.

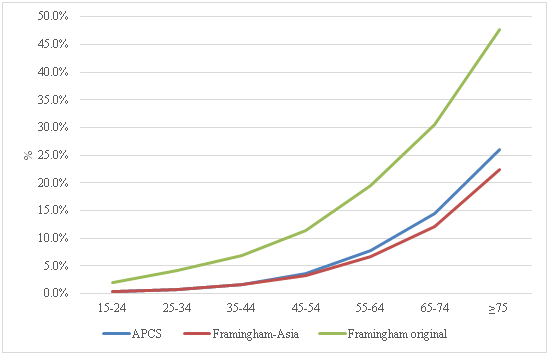
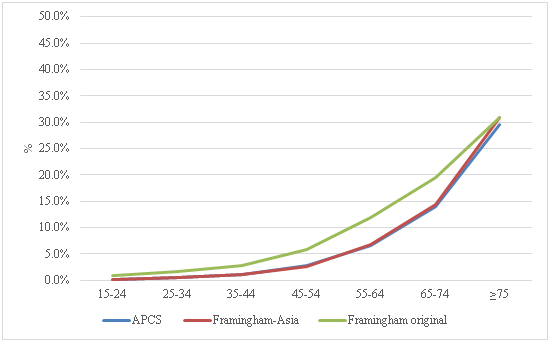
Figure ‎1 and Figure ‎2 compare the probability of CVD when applying the three differences equations, APCCS equation, Framingham-Asia equation and the original Framingham equation over an 8 to 10 years period. The APCS and Framingham-Asia equations calculate the risk of getting CVD for the next 8-years period, whilst the original Framingham equation calculates the CVD probability for the next 10 years.

Figure 1 The mean of 8-10 years probability of CVD in men who aged ≥ 15 years, NHESIV

Figure 2 The mean of 8-10 years probability of CVD in women who are aged ≥ 15 years, NHESIV.

Figure ‎1 shows the mean of CVD probability in Thai men. The original Framingham equation calculated the CVD probabilities as two times higher than the CVD probability that is computed using the APCS equation or the Framingham-Asia equation, in men. Overall the mean CVD probability in Thai men, when applying the original Framingham equation is 18.8% within a 10-period. While the APCS and the Framingham-Asia equations estimated the 8-year likelihood of getting CVD in men as 8.3% and 7.2% respectively; comparing across age groups, the trend of CVD probability increases with an increase in age. However, the original Framingham equation presents a higher likelihood of CVD than APCS or the Framingham-Asia equations in all age groups. Additionally, the trend of 8-year CVD probability is similar between the APCS equation and the Framingham-Asia equation at age 15 to 54. However, the 8-year CVD probability using the APCS is slightly higher than the Framingham-Asia equation at ages more than 55 years.   

Figure 2 shows the mean of CVD probability in Thai women aged 15 years and over when applying the APCS, Framingham-Asia and the original Framingham equations. The mean of CVD probability overall is 7.8% in the APCS equation, 8.1% in the Framingham-Asia equation and 11.1% in the original Framingham equation. The trend of CVD probability in women is similar when applying the APCS or the Framingham-Asia equations, which shows a higher CVD-probability in the older age groups. However, the original Framingham equation presents the higher probability than in APCS and Framingham-Asia equations, in all age groups. At ages 15 to 64, the CVD probability in the original Framingham equation is twice as high as APCS or the Framingham-Asia equations. In the senior women, at age 65 to 74, the CVD probability, when applied the original Framingham equation is 19.6%, the APCS equation 13.9% and the Framingham-Asia equation 14.4%.  Furthermore, at age 75 years and over, the CVD probability in women in all three equations are virtually the same, which are 29.5% in the APCS equation, 30.9% in the Framingham equation and 30.8% in the original Framingham equation

The estimated number of CVD events in the Thai population over 8 to 10 year periods

This section presents the estimated number of CVD events when multiplying the probability of CVD in an 8-year and 10-year period, to the number of the national mid-year population in Thailand in 2009. The number of CVD events, which have been calculated using three different equations, is the number of total CVD events which included both fatal and non-fatal events of IHD and stroke. Therefore, the number of estimated CVD events will deduct the number of people who are dead from CVD, to obtain the number of people who are alive with CVD. The number of deaths from CVD is estimated by applying the average of 10-year CVD mortality probability, which has been calculated from the national CVD mortality rate in Thailand over a 10-year period (1996-2006).

Figure 3 shows the estimated number of men who are alive with CVD in Thailand in 2017-2019. Overall, the APCS equation estimated 1.9 million, the Framingham Asia equation-estimated 1.6 million and the original Framingham equation estimated 4.4 million, of men who are alive with CVD. The graphs show that the original Framingham equation estimated a higher number of CVD events than either the APCS or the Framingham-Asia equations in all age group. The number of estimated CVD patients increase according to age groups. The APCS equation estimated the number of CVD cases as nearly the same at ages 15 to 44 years. However, at age 45 year and above, the APCS equation estimated number of CVD cases higher than the Framingham-Asia equation. The lowest number of CVD cases is at age 15 to 24 years. The number of CVD cases increases at age 45 years and above.  The highest number of CVD cases is at ages 65 to 74.

Figure 3 The estimated number of men who are alive with CVD in Thailand in 2017-2019

Figure 4 shows the estimated number of CVD cases in women in Thailand 2017 to 2019 when applying the 8-year and 10-year probability of CVD from the APCS equation, the Framingham-Asia equation and the original Framingham equation. The total number of estimated CVD cases in women are 2.7 million when applied the 10-year probability of CVD from the original Framingham equation, while, the Framingham-Asia equation estimated 2.0 million cases and the APCS equation estimated 1.9 million cases overall in an 8-year period. The graph shows that the original Framingham equation estimated a higher number of CVD cases in women than either the APCS equation or the Framingham-Asia equation in most age groups, except at age 75 and over. The lowest number of estimated CVD cases is at age 15 to 74 years. The APCS equation estimates the number of CVD cases in women higher than the Framingham-Asia equation from age 15 to 54 years.

Figure 4 The estimated number of women who are alive with CVD in Thailand during the next 8-10 years

On the other hand, the Framingham-Asia equation estimated the number of CVD cases higher than the APCS equation at age 55 years and above. The original Framingham equations estimated the highest number of CVD cases at age 65 to 74 years. However, at age 75 years and above the Framingham-Asia equation estimated the higher number of CVD cases than the original Framingham equation or the APCS equations.

The validation of the mathematical model

This section presents the validation of the mathematical model. The estimated number of people who are alive with CVD calculated from the APCS, the Framingham-Asia and the original Framingham equations have been validated against the actual number of CVD events in Thailand.

The national hospitalisation data in 2009 from NSO, Thailand, have been used to validate the model which covers the in-patient’s hospital admissions for the whole country. The in-patient’s admissions from the universal coverage health care scheme (UC), which accounts for 75% coverage of the all hospitalisation data in Thailand. The average number of the estimated CVD patients per year has been calculated to make it comparable with the 1-year hospital admissions in Thailand and is compared by age groups and gender. The CVD conditions have been identified by using the ICD-10 code, which I00-I99 refers to all CVD, I20-I25 refers to IHD and I60-I69 refers to stroke.

Figure ‎5 shows the validation of the estimated number of CVD patients among Thai men which has been calculated from the APCS equation, Framingham-Asia equation and the original Framingham equation. The actual number of hospital admission from CVD in 2009 in Thai men, has been used to validate the estimated number of CVD patients using each equation. The APCS and the Framingham-Asia equations estimated the total number of patients closer to the actual number than the original Framingham equation. The original Framingham equation overestimated the number of CVD patients by a factor of two.

Figure 5 Comparing the actual number of CVD hospital admissions with the estimated number of CVD patients in the 3 different equations amongst Thai men by age groups, in 2009

When comparing across age groups, the APCS equation and the Framingham-Asia equation underestimated the number of patients from age 15 to 54 years and overestimated the number of patients at age 65 years and over. The APCS equation and the Framingham Asia equation performed a close estimation at age 55 to 64 years.    

Although the original Framingham equation overestimated the number of CVD patients in almost all age groups, it performed a close estimation at age 45 to 54 years. However, the original Framingham equation overestimated the number of CVD patients as twice as high as the actual number at age 55 to 64 years and estimates are triple the exact numbers at age 65 to 74 years and 75 years and over.

Figure 5 Comparing the actual number of CVD hospital admissions with the estimated number of CVD patients in the three different equations amongst Thai men by age groups, in 2009

Figure 6 presents the comparison of the actual number of hospital admissions due to CVD and the estimated number of CVD patients when calculated using the APCS equation, the Framingham-Asia equation and the original Framingham equation, in women. Overall, the three equations overestimated the number of CVD patients in women. When comparing across age groups, all three equations underestimated the number of CVD patients at age 15 to 54 years. Also, at age 55 to 64 years, the APCS equation and the Framingham-Asia equation both closely estimate the actual number of CVD patients. Whereas, the original Framingham equation overestimated the number of CVD events. In the elderly age groups, all three equations have exceeded the number of CVD patients.

Figure 6 Comparing the actual number of CVD hospital admissions with the estimated number of CVD patients in 3 different equations among Thai women by age groups in 2009

Discussion

The probability of CVD events, which are calculated by the APCS equation, the Framingham-Asia equation and the original Framingham equation, increases accordingly with an increase in the age groups, in both men and women. However, the original Framingham equation projects a higher CVD probability than either the APCS equation or the Framingham-Asia equation, in both men and women at all age groups.  This might be because the original Framingham equation was derived from the Framingham cohort, who have different characteristics of CVD risk factors and ethnicity, compare to the Asian population. Many studies have found that the Framingham's function was suitable for predicting future CVD in middle-aged US white populations, and others with similar profiles of CVD risks.5,6 However, some studies showed an overestimated prediction for groups which have different risk profiles and ethnicity, such as Asian and some EU populations.7–9,17 The APCS equation was derived from the pooled data of the cohort studies around Asia and included the EGAT cohort study in Thailand. Hence, the Framingham-Asia equation was also recalibrated with the APCS cohort. Therefore, the APCS equation and the Framingham-Asia equation are more suitable than the original Framingham equation, when applied to the Thai population. 

When comparing genders, the original Framingham equation calculated the higher probability of CVD in men than in women. Conversely, the likelihood of CVD in women is higher than in men in the Framingham Asia equation. This might because the Framingham Asia equation was reported to overestimate the risk of CVD by an average 4% in women and underestimate the CVD risk by an average 2% in men, in the non-Chinese cohorts.16  Also, the prevalence of regular smoking in women is lower than in men, which might have an impact and affect the calculations. There are some metabolic risk factors in women which are higher than men. For example, the mean of BMI in men and women is 23 kg/m2 and 24.36 kg/m2 respectively. The mean of total cholesterol in women and men are respectively, 5.58 mmol, and 5.27 mmol. Hence, the prevalence of diabetes in women is 10.9% but in men is 9.3%.

Concerning the mathematical equations, there are some limitations of using the APCS equation, the Framingham-Asia equation and the original Framingham equation. Firstly, the type of mathematical models is different. The APCS equation and the Framingham-Asia applied the Cox's model, but the original Framingham equation was derived from the Weibull's model. Secondly, the input parameters of the risk factors in the APCs, and the Framingham-Asia equations are limited because the APCS and the Framingham-Asia were trying to derive equations that can be used with the limited sources of information and also apply to many countries around Asia. Therefore, the APCS and the Framingham-Asia equation used BMI, age, gender, blood pressure and total cholesterol to project the CVD events.

On the other hand, the original Framingham equation included all of those variables and diabetes status, which is another potential risk factor of CVD. Thirdly, the time frame differences, the APCS and the Framingham Asia equations are both based on an 8-years cohort study, while the original Framingham equation is based on 10-years of the follow-up period. Therefore, when conducting the validation of the mathematical models, the average number of CVD patients per year has been used to compare the number of actual CVD hospital admissions in a single year.

In term of the outcome limitations, the APCS equation and the Framingham-Asia equation estimated only the number of all CVD events but cannot predict the CVD conditions separately. The original Framingham equation is more flexible in being able to calculate the CVD events separately for IHD or Stroke. However, all three equations calculate both fatal and non-fatal events together, which cannot identify the exact number of people who die from or are alive with CVD. Therefore, the CVD mortality probability is applied to the number of all CVD events, to get the number of people who are likely to die from CVD. Then, deduct this number from the number of all CVD events to obtain the number of people who are alive with a CVD condition.

When validating the equations against the actual number of hospital admissions due to CVD in Thailand, the APCS equation and the Asia-Framingham equation both jointly estimated the total number of CVD patients. The original Framingham equation overestimated the total number of CVD patients in both men and women. However, all three equations underestimated the risk in the young adult population and exceeded the uncertainty in the older community, because the CVD risk equations are derived from the middle age group's people. The APCS and the Framingham Asia equations are derived from cohort's age 30 to 75 years. The original Framingham equation was derived from cohorts aged 30 to 62 years. When applying them to the younger age groups, they might underestimate the CVD events. Additionally, the younger generation in Thailand may have a different lifestyle than the older generation, such as undertaking less physical activity and an unhealthy diet.  Moreover, there are a limited number of studies that derived CVD risk equations for a population aged less than 30 years old.

Furthermore, there are some limitations on the availability of data in Thailand for undertaking the validation. As mention above, The Chronic disease surveillance system did not capture all CVD events for the whole country.  The data only included out-patients admissions in public hospitals in 43 provinces, which was not segregated by gender. Hence, the number of CVD patients is not available to compare by gender. The number of in-patients hospitalisation data covered 75% of the hospital admissions in Thailand. This data, however, did not take account of approximately 8% of the Thai population who are in the social security health care scheme, 8% who are in the civil servant health care scheme and the other 9% who are in the private health insurance system, for which data was not available to access.

Regarding the mortality data, the number of deaths from CVD may be underestimated, because the average 10-year CVD mortality probability has been calculated from the national CVD mortality rate in Thailand during 1996 to 2006, but the estimation is based on the year 2009. Hence, the death registry in Thailand might be under-reporting or miss classifying the causes of death in its data. Moreover, the CVD mortality rate in 2009 was presented as a total mortality rate, but not given by age groups and gender. Therefore, the 10-years mortality from 1996 to 2006 was used instead because it was the best available data during the period of this study.        

Conclusions

The original Framingham equation overestimated the risk of CVD in the Thai population in all age groups. The APCS and the Framingham-Asia equation both performed better estimation than the original Framingham equation in both men and women.

Conflict of interest statement

The authors declare that there are no conflicts of interest.

Appendix

The main outcome prediction is the of probabilities of CVD related events, such as stroke, heart attacks and heart failure.Details of the equations are described below.

The APCS cohort equation
The Asia cohort CVD risk prediction equations (APCS equation)
The probability of getting a cardiovascular event within 8 years in Asian men is:

$p{(8)}_{men}=1-s{(8)}_{men}\exp \{0.065(ag{e}_i-\overline{age})+0.027(SB{P}_i-\overline{SBP})+0.095(T{C}_i-\overline{TC})+0.33(smok{e}_i-\overline{smoke})\}$

Equation.1
For Asian women is:
$p{(8)}_{women}=1-s{(8)}_{women}\exp \{0.072(ag{e}_i-\overline{age})+0.023(SB{P}_i-\overline{SBP})+0.027(T{C}_i-\overline{TC})+0.31(smok{e}_i-\overline{smoke})\}$

Equation 2

1. The Framingham’s equation for estimating the probability of getting a cardiovascular event within 8 years (Framingham’s Asia)

For men is:
$p{(8)}_{men}=1-s{(8)}_{men}\exp \{0.068(ag{e}_i-\overline{age})+0.021(SB{P}_i-\overline{SBP})+0.015(T{C}_i-\overline{TC})+0.37(smok{e}_i-\overline{smoke})\}$

Equation ‎3
For women is
$p{(8)}_{women}=1-s{(8)}_{women}\exp \{0.078(ag{e}_i-\overline{age})+0.017(SB{P}_i-\overline{SBP})+0.014(T{C}_i-\overline{TC})+0.55(smok{e}_i-\overline{smoke})\}$
Equation 4
When:
$s(8)$ = The survival free from the cardiovascular event. (in the 8 years average)
$\overline{age}$ = The mean age of the NHESIV participants
$ag{e}_i$ = The age of the individual
$\overline{SBP}$ = The mean systolic blood pressure of the NHESIV participants
$SB{P}_i$  = The systolic blood pressure of the individual
$\overline{TC}$    = The mean of total cholesterol of the NHESIV participants
$T{C}_i$    = The total cholesterol of the individual
$\overline{smoke}$ = The prevalence of regular smoking of the NHESIV participants
$smok{e}_i$ = The smoking status of the individual (1=being a regular smoker, 0=not smoking)
3) The Framingham’s equation (Framingham original)
Using the Framingham's equation for the Thai population from Weibull accelerated failure-time model regression coefficients.16

               
$m=\text{constant}1+{\displaystyle {\sum }_{i=1}^{i=n}{B}_i}{x}_i$            Equation 5

$CVDrisk=1-(1-p_{ihd})(1-p_{stroke})$            Equation 8

when; m is the interim variables
$x_i$            are the risk factors
$\beta$ are coefficients estimated from the Framingham study
$u$ is the interim variables (Is this the same as m above?)
$t$ is the time of follow-up in years
$p$  is the predicted probability of IHD/Stroke by time t

Eq1        $m=8.39-0.37age-0.005TC-0.461CM-0.009SBP-0.384SM$
Eq2         $u=\log 10-\frac{m}{0.82}$

Female IHD risk at 10 years

Eq1         $m=9.32-0.036age-0.006TC-0.695DM-0.01SBP-0.221SM$
Eq2         $u=\log 10-\frac{m}{0.83}$

Male Stroke risk at 10 years             
Eq1         $m=12.70-0.081age-0.391DM-0.019SBP-0.413SM$
Eq2        $u=\log 10-\frac{m}{0.87}$

Female Stroke risk at 10 years         
Eq1         $m=11.25-0.06age-0.684DM-0.017SBP-0.488SM$
Eq2        $u=\log 10-\frac{m}{0.83}$

References

1. Sritara P, Cheepudomwit S, Chapman N, et al. Twelve-year changes in vascular risk factors and their associations with mortality in a cohort of 3499 Thais: the Electricity Generating Authority of Thailand Study. Int J Epidemiol. 2003;32(3):461–468.
2. Wilson PW, D’Agostino RB, Levy D, Belanger AM, Silbershatz H, Kannel WB. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97(18):1837–1847.
3. Cui J. Overview of risk prediction models in cardiovascular disease research. Ann Epidemiol. 2009;19(10):711–717.
4. Wu Y, Liu X, Li X, et al. Estimation of 10-year risk of fatal and nonfatal ischemic cardiovascular diseases in Chinese adults. Circulation. 2006;114(21):2217–2225.
5. Group DPC. Prediction of mortality from coronary heart disease among diverse populations: is there a common predictive function? Heart. 2002;88(3):222.
6. Liao Y, McGee DL, Cooper RS, Sutkowski MBE. How generalizable are coronary risk prediction models? Comparison of Framingham and two national cohorts. Am Heart J. 1999;137(5):837–845.
7. Liu J, Hong Y, D’Agostino Sr RB, et al. Predictive value for the Chinese population of the Framingham CHD risk assessment tool compared with the Chinese Multi-Provincial Cohort Study. Jama. 2004;291(21):2591–2599.
8. Thomsen TF, McGee D, Davidsen M, Jørgensen T. A cross-validation of risk-scores for coronary heart disease mortality based on data from the Glostrup Population Studies and Framingham Heart Study. Int J Epidemiol. 2002;31(4):817–822.
9. Haq IU, Ramsay LE, Yeo WW, Jackson PR, Wallis EJ. Is the Framingham risk function valid for northern European populations? A comparison of methods for estimating absolute coronary risk in high risk men. Heart. 1999;81(1):40–46.
10. Brindle P, Jonathan E, Lampe F, et al. Predictive accuracy of the Framingham coronary risk score in British men: prospective cohort study. Bmj. 2003;327(7426):1267.
11. Hippisley-Cox J, Coupland C, Vinogradova Y, Robson J, May M, Brindle P. Derivation and validation of QRISK, a new cardiovascular disease risk score for the United Kingdom: prospective open cohort study. Bmj. 2007;335(7611):136.
12. The Asia Pacific Cohort Studies Collaboration. Cholesterol, diabetes and major cardiovascular diseases in the Asia-Pacific region. Diabetologia. 2007;50(11):2289–2297.
13. Vathesatogkit P, Woodward M, Tanomsup S, et al. Cohort profile: the electricity generating authority of Thailand study. Int J Epidemiol. 2011;41(2):359–365.
14. Supalerk Pattanaprichakul MD, Sutipong Jongjirasiri MD, Sukit Yamwong MD. RAMA-EGAT Risk Score for Predicting Coronary Artery Disease Evaluated by 64-Slice CT Angiography.
15. The Asia Pacific Cohort Studies Collaboration. Cardiovascular risk prediction tools for populations in Asia. J Epidemiol Community Health. 2007;61(2):115–121.
16. Khonputsa P, Veerman JL, Bertram M, et al. Recalibration of the Framingham equations in the Thai population. 2011.
17. Brindle P, Beswick A, Fahey T, Ebrahim S. Accuracy and impact of risk assessment in the primary prevention of cardiovascular disease: a systematic review. Heart. 2007;92(12):1752–1759.