Introduction

Wellbore trajectory planning is essentialfor designing directional and horizontal drilling. Its importance appears especially in cases of multi-well platforms in which a number of aspectshave to be carefully examined before designing the final well path to target.Fundamental mathematical formulations to expresschanges in the vertical and horizontal planes, wellbore curvature, dogleg severity calculations, directional-well profiles, horizontal well profiles, and three-dimensional well profiles for a wellbore trajectory were presented by Azar and Samuel,¹ Mitchell,² Bourgoyn,³Hossain and Al-Majed,⁴ Rabia,⁵ and Mitchell and Miska.⁶For wellbore trajectory planning, a quite number of important terms are used:KOP,TVD, MD, end of buildup (EOB), hold angle, the tangent sections, start of drop, end of drop, target displacement, target location, drop off rate (DOR), build up rate (BUR), turn rate, dog-leg severity (DLS), horizontal displacement (HD), vertical section (VS), geographic north, grid north, magnetic north,  horizontal turn rate, hole inclination (j), azimuth angle (ϑ), direction angle, coordinates of surface and targets, and declination angle. In well-trajectory design, the targets are usually determined by the geologist with acceptable tolerance (e.g. a circle of radius 100 feet having the target as its center). In order to reach the target, target zones must be selected as large as possible. If there are multiple zones to be reached, the planned trajectory should be reasonable and be achieved without causing drilling problems, such as those experienced in our case study.⁴

A good understanding of the definitions of the above terms, their derivatives and calculations, is essential for selecting good practical directional profilesand for overcoming the resulting problems.

In this paper, horizontal wellbore trajectory is going to be optimized by selecting improved horizontal hole profile, KOP, horizontal turn trajectory, vertical turn determination, mud density, and the best surveying method which is suitable for building 3D profiles. Additionally, wellbore stability analysis models, geomechanical earth models (GEM), and stress determination have to be taken in consideration in order to choose the best orientation for wellbore that yields no major hole problems. 

Horizontal well profiles

Horizontal wells are drilled through curved sections up to a 90°angle and then horizontally into the formation. In practical applications, horizontal well inclination angles are approximately 80 to 100°. In an ideal horizontal well, the inclination angle is 90°. The three pattern classifications of horizontal holes are short (with a radius of curvature 30–200 ft.), medium (200–1,000 ft.), and long turn radius (1,000–3,000 ft.) patterns. There are also ultrashort-radius systems in which high-pressure jetting techniques are used to turn the well from a vertical to a horizontal orientation.^1–5In general, the main factors affecting a horizontal-well profile were presented by Mitchell and Miska.⁶

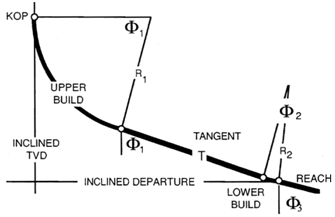
Horizontal well profile (Figure 1) consists of a vertical segment, a first buildup segment, a tangent part, and a second buildup segment, followed by a horizontal section. Here, the departure is defined as the displacement from vertical until the well reaches the beginning of the horizontal section. Horizontal displacement is the sum of the length of the horizontal section and the departure. Some horizontal wells consist of one build section connecting the vertical part with a horizontal section. The mathematical trajectory planning calculations and equations are the same as those used in directional calculations presented by Azar and Samuel,¹ Mitchell,² Bourgoyn,³ Hossain and Al-Majed,⁴ Rabia,⁵ and Mitchell and Miska.⁶However, there is an exception that the primary unknown in the combination trajectory plan is the depth of KOP.Additionally, other problems appeared in horizontal turn trajectory, vertical turn computations, mud weight selection, 3D profile building and survey methods selection are addressed in the following sections.

Figure 1 Horizontal well profile.

KOP, horizontal turn trajectory, and verticalturn determination 

Mitchell² presented the mathematical equations for calculating KOP in the combination trajectory horizontal well planning as follows:

$\text{Inclined TVD}={\text{R}}_1\sin {\text{φ}}_1+\text{T}\cos \cos {\text{φ}}_1+{\text{R}}_2\left(\sin {\text{φ}}_3-\sin {\text{φ}}_1\right)$ (1)

$\text{Inclined DEP}={\text{R}}_1\left(1-\cos {\text{φ}}_1\right)+\text{T}\sin \sin {\text{φ}}_1+{\text{R}}_2\left(\cos {\text{φ}}_1-\cos {\text{φ}}_3\right)$ (2)

$\text{Inclined MD}={\text{R}}_1{\text{φ}}_1+\text{T}+{\text{R}}_2{\text{φ}}_2$ (3)

$\text{Departure of the REACH}={\text{REACH x sinφ}}_3$ (4)

$\text{Change in TVD of the REACH}={\text{REACH x cosφ}}_3$ (5)

Where:

Reach = The along the hole distance (MD) of portion of the hole which is normal thought to be horizontal

MD = Measured depth, ft.

Dep = Departure length, ft.

T= Tangent length, ft.

R₁= Radius of curvature for upper build, ft.

R₂= Radius of curvature for lower build, ft.

j = Inclination angle for position 1, 2, and 3 (j₃=90^o), degrees

Figure 1 shows the various terms and abbreviations given in these equations, which and can be solved simultaneously to determine KOP. The resulting problems during planning a horizontal turn and vertical turn in the horizontal section of the planned wellbore can be determined and solve during Mitchell² mathematical equations and programs.

Selection of mud weights for horizontal wellbore

Mud weight selection methods used in vertical wellscannot be used in directional or horizontal holes. Therefore, Mitchell² suggested the following equation for selecting mud densities (ppg) to stabilize drill holes:

$M{W}_{horizontal}=M{W}_{vertical}+\left(OBW-LOT\right)\frac{1-\cos 2\phi }{1.6}$ (6)

Where:

WM= Mud weight, ppg

OBW = Overburden weight (Overburden stress), ppg 

LOT= Leak off test value, ppg    

j= Inclination, degrees

Three dimensional well profiles for a wellbore trajectory

The design planning of the wellbore is required to construct a smooth 3D path that connects a surface or subsurface location to a known target or targets. In addition to 3D geometric requirements, the designer must also consider other factors related to the drilling process, such as drill string mechanical integrity, wellbore stability, cuttings transport, cementing and perforating operations, and running of casing.⁶For the purpose of well-path optimization, minimum drilling cost or minimum drilling time is usually used as the optimization criterion. The design process frequently requires a few iterations before the desired solution is found. Five methods can be used to design a 3D well path. The five methods [11] are average angle method (AAM), radius of curvature (RCM), constant build and turn rate (CBTM), constant curvature and build rate (CCBM) (constant tool face), and minimum curvature method (MCM). 3D geometric considerations and a discussion of these methods are presented by Azar and Samuel,¹ Mitchell,² Bourgoyn,³ Hossain and Al-Majed,⁴ Rabia,⁵ and Mitchell and Miska.⁶However, MCM is the most commonly used by the petroleum industry for both well trajectory planning and directional survey evaluation.⁶

The Minimum Curvature Method (MCM)

MCM was originally proposed by Taylor and Mason⁷ and by Zaremba⁸ as a way to improve directional-survey analyses. Zaremba used the term circular-arc method and carried out the development using the method of vectors. Recently, Sawaryn and Thorogood⁹ published useful algorithms for directional well planning and deflection tool orientation. The final MCM equations which were used in optimizing wellbore trajectory are:

$RF=\frac{\Delta MD}{\beta }\tan \frac{\beta }{2}$ (7)

$\Delta X=\left(\sin {\phi }_1\cos {\vartheta }_1+\sin {\phi }_2\cos {\vartheta }_2\right)RF$ (8)

$\Delta Y=\left(\sin {\phi }_1\sin {\vartheta }_1+\sin {\phi }_2\sin {\vartheta }_2\right)RF$ (9)

$\Delta Z=\left(\cos {\phi }_1+\cos {\phi }_2\right)RF$ (10)

Where

RF= Ratio Factor

b= Dog-leg angle, degrees

j=inclination angle, degrees

ϑ=Azimuth angle, degrees

Wellbore Trajectory Optimization

Trajectory optimization is a fundamental aspect of a wellbore design. An optimized wellbore trajectory enables drilling to be performed under minimum geostress loads and promotes a longer service life for wellbores. Trajectory optimization is particularly significant to projects in which wellbores are designed with reference to a given platform. Consequently, the necessity for trajectory optimization increases with the constraint of a fixed surface location to an irregular reservoir geometry. Despite the importance of trajectory optimization, the published articles on this subject are scarce or not available. In this work, several methods are adopted to evaluate the advantages of each possible choice of wellbore trajectory. A key issue is the choice of mechanical insitu stresses as an index for determining wellbore stability. Hole is planned from offset well data (s_v, s_hmin, log correlations to strength data, p_o, and logs data). To increase wellbore stability, the best well orientation is that which minimizes the principal stress difference normal to the axis. In a relaxed (non-tectonic) basin where (s_v>s_hmin~ s_HMAX), vertical wells are the most stable wellbores. In other words, vertical holes are subjected to lower shear stresses; therefore they are generally more stable than horizontal holes.In a tectonic basin, the best well orientation is practically dependent on insitu stresses estimation. For example:If s_HMAX>s_v>s_hmin, we still have to know the specific values to decide the best trajectory, If s_HMAX = 0.75 psi/ft, s_v = 0.56 psi/ft, s_hmin = 0.44 psi/ft., ahorizontal well parallel to s_HMAX is the best optimized profile, and If s_HMAX = 0.75, s_v = 0.65, s_hmin = 0.44 psi/ft., a horizontal holeparallel to s_hmin is likely the best optimized wellbore. Consequently, careful rock mechanics analysis is the bestmethod for wellbore trajectory selection.  Thebest orientation which minimizes the principal stressdifference normal to the axis increases wellbore stability. To predict rock mechanics stability, Mitchell² presenteda borehole stability method for vertical and inclined wells, and the general methodology for analysis of wellbore stability has already been discussed. Yi et al.¹⁰ built the GEM to predict wellbore stabilityusing the following equations to determine insitu stresses:

${\sigma }_v=\underset{0}{\overset{H}{{\displaystyle \int }}}{\rho }_b\left(h\right)dh$ (11)

${\sigma }_h=\frac{\upsilon }{1-\upsilon }\left({\sigma }_v-{\alpha }_b{P}_p\right)+{\alpha }_b{P}_p$ (12)

Where

s_v= Overburden stress, psi

s_h= Minimum horizontal stress, psi

ρ_b= Bulk density for rock, lb/ft.³

h= depth, ft.

υ= Possion’s ratio

α_b= Biot Coefficient

P_p= Pore pressure, psi

Maximum horizontal stress magnitude and orientation can be determined from the inversion of calibration of borehole failure such as breakouts, washouts, drilling induced fractures and drilling problems.¹⁰ Additionally, wellbore stability models used for horizontal and deviated wells are presented by Manshad et al.,¹¹Mohiuddin et al.,¹² and Yi et al.,¹⁰. The role of rock strength criteria in wellbore stability and trajectory optimization is presented by Chabook et al.¹³ A combination of all above mentioned methods will be used to stabilize and optimize the horizontal wellbore.

Horizontal Well Data

Horizontal wellbore is required to drill 12.25" hole vertical to 6200 ft. then start building to 39.83° inclination along 177.83°azimuth at 7192 ft. with 4°dog-leg, then keep holding with the same inclination and azimuth to 7404 ft. Drilling was continued for building curve section in 8 1/2'' hole with 5.5°dog-leg to landing point at MD = 8519 ft., TVD = 7773.4 ft.and with 88° inclination along 132°azimuth. After that,keep holding with same to 8608.9 ft., and start building with 1.5°dog-leg till building 89° inclination along 128° azimuth until reaching to 9979 ft. horizontally.Formation tops, MCM calculations, and casing points selection for planned horizontal well passed through 5 targets after applying the above methods are shown in Figure (2) and Table (1).More details of the horizontal well data are published by Halafawi and Avram.¹⁴

Figure 2 Formation Tops, side view, plan view, and casing points for planned horizontal well passed through 5 targets

Results and Discussion

In well-trajectory design, the coordinates of the initial point and target-point are selected to pass through 5 targets: NRQ 255 6H-1, NRQ 255 6H-2, NRQ 255 6H-3, NRQ 255 6H-4, and NRQ 255 6H-5. Using MCM to build the optimum survey trajectory for horizontal hole,  it resulted in MD= 8560.5 ft.,  I=88°, A=133°, TVD=7773.4 ft. for NRQ 255 6H-1; MD= 9024.8 ft.,  I=90.92°, A=128.28° TVD=7778.4 ft. for NRQ 255 6H-2; MD= 9373.9 ft.,  I=90.80°, A=126.28°, TVD=7773.4 ft. for NRQ 255 6H-3; MD= 9613.8 ft.,  I=87.72°, A=127.23°, TVD=7778.4 ft. for NRQ 255 6H-4; and MD= 10021 ft.,  I=89.11°, A=128.78°, TVD=7786.4 ft. for NRQ 255 6H-5. Vertical side view, plan view, and casing points are shown in Figure 2 for the planned horizontal wellbore.

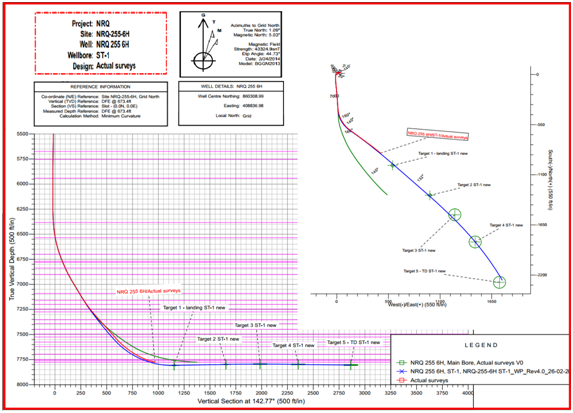
Tables 1-3 show MCM calculations and results for horizontal wellbore surveying. Figures 3-5 show the planned wellbore trajectory versus the real trajectory for drilling each casing point section. There is no difference between the planned and the real trajectories for sections 1 and 2 where 13.375’’ (13 3/8") and 9.625’’ (9 5/8") casings are landed to TVD=  4694.1 ft., MD=4695 ft.and TVD=7230 ft. MD=7343.6 ft. respectively (Figure 3). Therefore, the design wellbore trajectory is optimum without major instability problems until MD=7343.6 ft.

Figure 3 Formation Tops, side view, plan view, and casing points for horizontal wellbore- the planned versus the reality- section 1and section 2

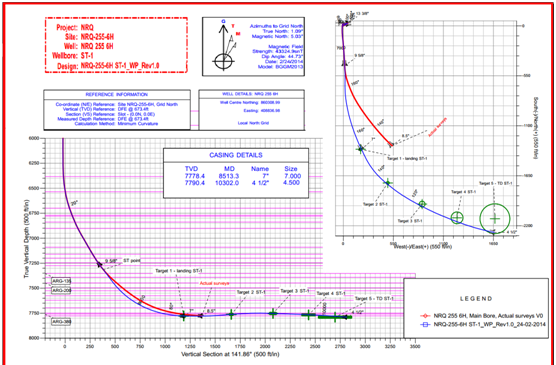
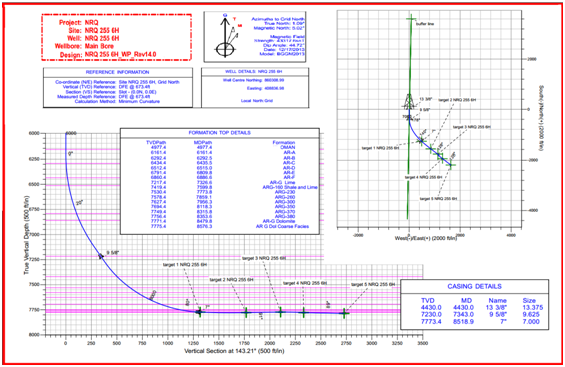
Figure 4 Sidetracking hole, side view, plan view, and casing points for horizontal well- the planned versus the reality- section 3

Figure 5 Final horizontal well trajectory- the planned versus the reality

MD	j	ϑ	TVD	+ N/-S	+ E/-W	Dleg	TFace	VSectTarget
7306	37.57	177.17	7203.2	-375.3	11.1	0	0	305.5
7321	38.86	175.14	7215	-384.5	11.7	12	-45	313.3
7341	38.86	175.14	7230.5	-397	12.8	0	0	323.9
7766.1	43	125	7560.4	-619.1	146.4	7.64	-102.8	581.5
8420.4	91.08	131.69	7808.4	-986.7	600.8	7.4	8.95	1149.1	Target 1 ST-1
8510.4	91.08	131.69	7806.7	-1046.6	668	0	0	1237.4
8527.8	91.12	131.95	7806.4	-1058.2	681	1.5	82.22	1254.6
8935.1	91.12	131.95	7798.4	-1330.4	983.8	0	0	1654.5	Target 2  ST-1
9116.8	90.28	134.54	7796.2	-1454.9	1116.2	1.5	107.89	1833.7
9274.8	90.28	134.54	7795.4	-1565.7	1228.8	0	0	1990	Target 3 ST-1
9579.4	88.99	140.5	7797.3	-1790.2	1434.4	2	102.22	2293.2
9640.3	88.99	140.5	7798.4	-1837.2	1473.1	0	0	2354.1	Target 4 ST-1
10062.5	89.56	148.92	7803.7	-2181.5	1716.8	2	86.22	2775.6
10148.1	89.56	148.92	7804.4	-2254.8	1761	0	0	2860.7	Target 1 ST-1

Table 2 MCM calculations and results for horizontal wellbore section 1 and 2.

MD	j	ϑ	TVD	+ N/-S	+ E/-W	Dleg	TFace	VSectTarget
7306	37.57	177.17	7203.2	-375.3	11.1	0	0	307.2
7402	41.5	177.17	7277.2	-436.3	14.1	4.09	0	357.9
7460	41.5	177.17	7320.7	-474.7	16	0	0	389.7
8452	85.7	134.5	7767	-1211.9	419	5.76	-53.54	1221.5
8552.6	87	132	7773.4	-1280.6	492.1	2.8	-62.56	1320.3
8642.6	87	132	7778.1	-1340.7	558.9	0	0	1408.4
8923.8	91.77	129.01	7781.2	-1523.3	772.6	2	-32.11	1682.7
9013.1	91.77	129.01	7778.4	-1579.5	842	0	0	1769.2	target 2
9256.5	90.31	125.14	7774	-1726.2	1036.1	1.7	-110.6	2002.9
9364	90.31	125.14	7773.4	-1788.1	1124	0	0	2105.1	target 3
9541.5	87.94	127.78	7776.1	-1893.5	1266.7	2	131.86	2275
9605.5	87.94	127.78	7778.4	-1932.7	1317.3	0	0	2336.6	target 4
9695.6	88.98	128.65	7780.8	-1988.4	1388.1	1.5	39.67	2423.7
10010.4	88.98	128.65	7786.4	-2185	1633.9	0	0	2728.3	target 5

Table 3 MCM calculations and results for sidetracking hole

During drilling 8.5” casing hole, the drillstring was stuck. Firstly, during drilling 8.5” hole; and after the driller performed the following actions:

• Picking up (P/U) in 8 1/2" hole
• Reaming bottom hole assembly (BHA) after 7" Liner (LNR) got held-up @ 8240’ MD, Pulling out of hole (POOH)with LNR
• Re-Runing Tricone Insert (RR TCI) Bit size 8 1/2" dressed with 3 x 18 Jets and 6 3/4" measurement while drilling (MWD) tools,

Then, the shallow testwas done and found OK. Secondly, during runningin hole to 7780ft., a resistance was found. After the decision was to ream down with 40RPM, 490gpm, SPP 3050psi, and 3000-5000ft./lb to 8070 ft. and make circulation as a first action to remediate the problem, shaker was found continuously loaded with lumps of caved shale. Several pack offs were also noticed. After that, Resuming harder reaming down as a second action to rapidly treat the problem, but shaker was also found continuously heavily loaded with shale lumps, several pack offs were also noticed, and sudden severe mud losses at 8290ft. were also occurred. Finally, POOH for cement plug decision was taken to pump two cement plugs. The cement was then drilled to 7305ft. Whipstock was run in hole and a window from 7305 to 7315ft. 4 ft.was milled of the new formation was drilled to 7719ft. (the last foot drilled in 3 hrs). Sidetracking happened due to poor wellbore stability determination (Figure 4).

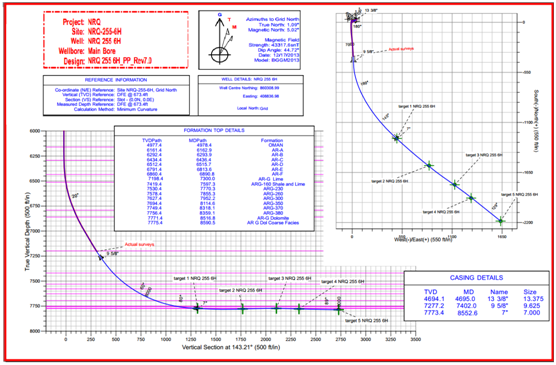
However, logging while drilling (LWD) data and drilling data were used to build new a GEM and wellbore stability model accompanied by MCM to optimize and update sidetracking profile to enter the five targets horizontally. In-situ stresses (s_x, s_y, s_z) were, firstly, determined, these stresses were transferred to radial stresses (s_r, s_q, s_z), the GEM was constructed, and then the best wellbore orientation was selected.Finally, the safe mud window was determined and the optimum trajectory was selected. After updating wellbore stability for wellbore,the 6’’ sidetracking wellbore entered the 5 targets horizontally at MD= 10010.4 ft., I=88.89°, A=128.65°, TVD=7786.4 ft. as planned without any other major instability problems as shown in Figures 4 and 5.The planned horizontal trajectory became matched with the real trajectory (Figure 5).